水模拟

烟雾、海浪、水滴…，这些司空见怪的自然现象其实有着非常复杂的数学规律，对于流体的研究，有两种完全不同的视角，分别是欧拉视角和拉格朗日视角。欧拉视角的坐标系是固定的，如同站在河边观察河水的流动一样，用这种视角分析流体需要建立网格单元，还会涉及到有限元等复杂的工程方法，一般用在离线的应用中。而拉格朗日视角则将流体视为流动的单元，例如将一片羽毛放入风中，那么羽毛的轨迹可以帮我们指示空气的流动规律。

N-S方程及SPH

这类算法是典型的拉格朗日视角，它的基本原理就是通过粒子模拟流体的运动规律，然后再转换成网格进行流体渲染。

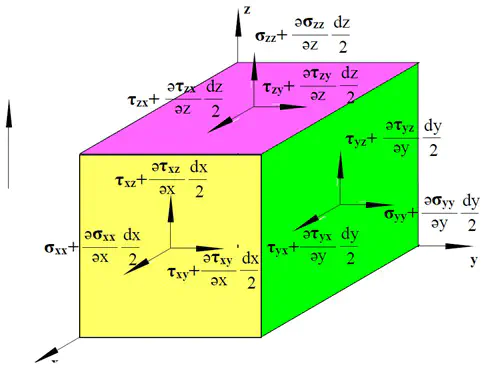
N-S方程(Navier-Stokes)
主要描述的就是这么几个力(推导可参考¹)：

1. 作用在单元体上的力
2. 质量力：重力，惯性力
3. 表面力：压力，切力

SPH(Smoothed particle hydrodynamics)
对上述的N-S方程进行了简化实践，用了一个“光滑核”函数算相互作用力。

和其他流体力学中的数学方法类似，SPH算法同样涉及到“光滑核”的概念，可以这样理解这个概念，粒子的属性都会“扩散”到周围，并且随着距离的增加影响逐渐变小，这种随着距离而衰减的函数被称为“光滑核”函数，最大影响半径为“光滑核半径”

下面是我之前转载在GAD的 (没错，我的另一个马甲号)， 原作者是搜狐畅游的CTO，原站已废： SPH算法简介（一）: 数学基础 SPH算法简介（二）: 粒子受力分析 SPH算法简介（三）: 光滑核函数 SPH算法简介（四）:Hello,SPH SPH算法简介（五）：表面张力的计算

粒子模拟还可以参考liquidfun这个项目²。 这里有个视频³，相当惊艳。

欧拉法视角

常用的UV动画了，不解释了：

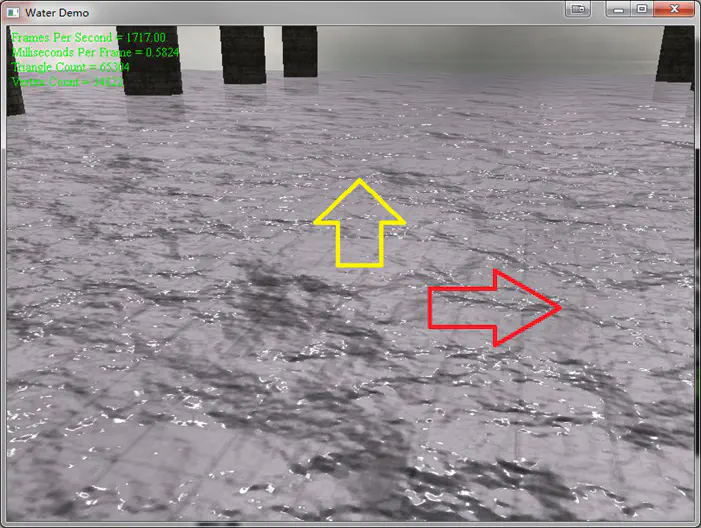
这个是我基于纹理实现的一个波动效果，一张displacement搞定： displacement这类方法的好处：比较容易实现受外界影响的波动效果

FFT

首先是作者思路，或者说论文套路，为什么这么做，著名的[choppy waves]⁴： 水波(重力波) -> 哈密顿系统 -> 稳定系统 –> 有周期解 –> 莫非三角函数？ -> 拿业内标准FFT处理处理

算法核心点在于频谱的处理，公式这里就不推了，偏经验模型⁵。

首先用一个经验分布加上高斯噪声：

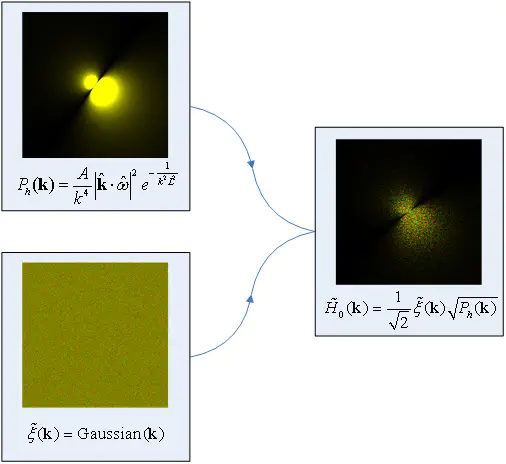
而后和时间项进行卷积，随时间旋转，来几次IFFT，得到displacement：

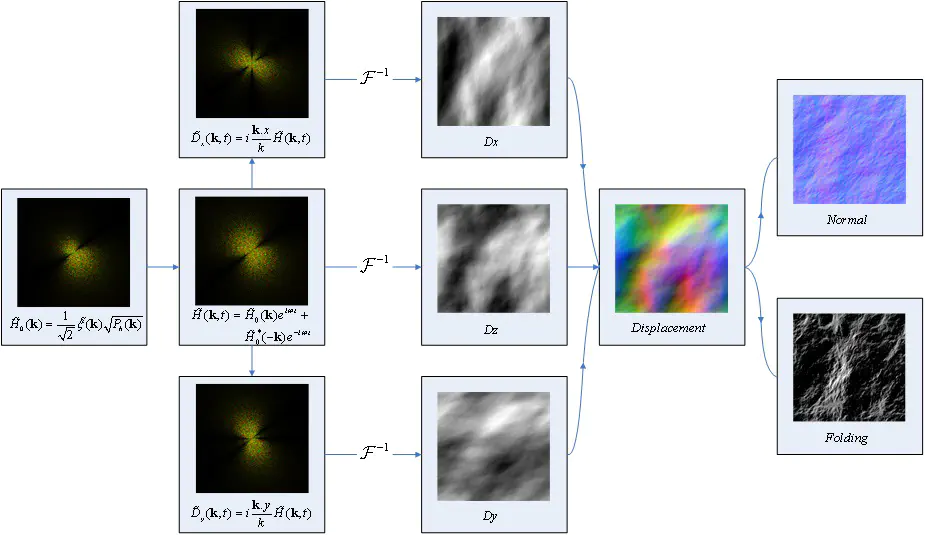
FFT实现

参考这篇⁶，相当完美，作者也给出了Demo⁷

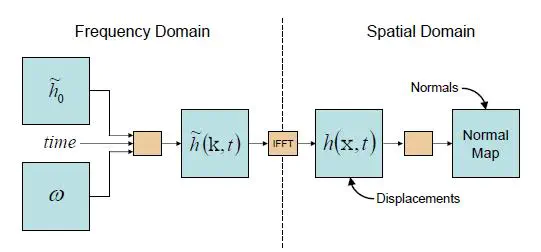主要步骤就是：生成频谱->加噪声->频谱旋转->IFFT

LOD
由于写Demo可以忽略游戏框架，方便起见将置换贴图做到屏幕空间：

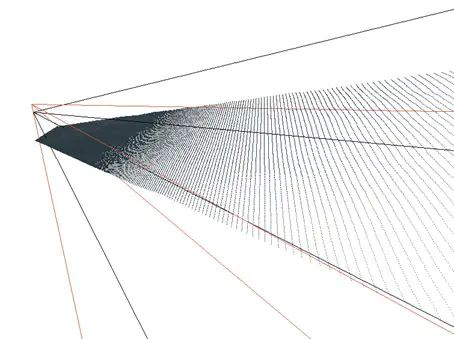
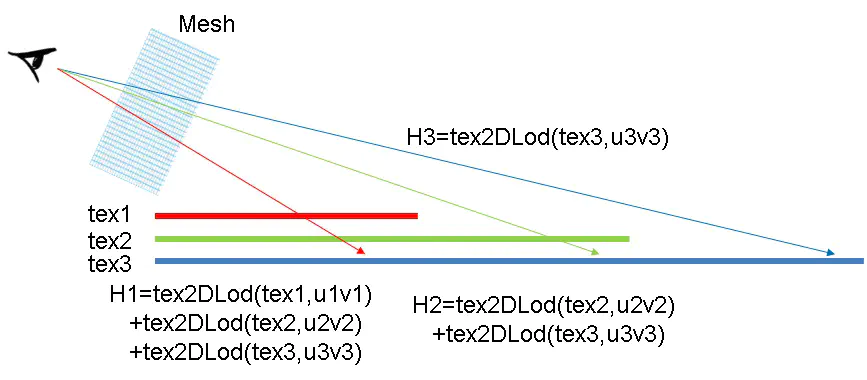
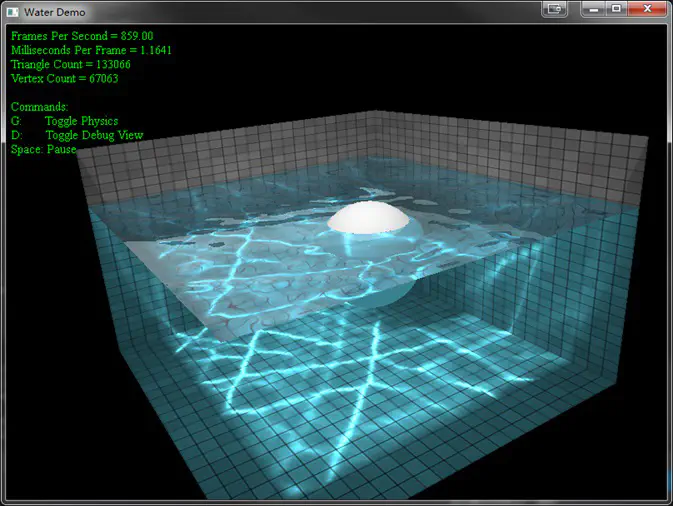
最终结果
只做了mesh部分 :)

其他

水波作用力⁸：${\displaystyle q={\dfrac {\rho ,u^{2}}{2}}}$

$q;$ = dynamic pressure in pascals, $\rho ;$ = fluid density in kg/m3 (e.g. density of water), ${\displaystyle u;}$ = flow speed in m/s.

除此之外还有：泡沫，浪花，光照，物理，水压力及拖尾，，，以后再说吧 :)