Variance Depth Map

很早就想总结下这类upsample算法。

准备工作

参考论文¹，利用硬件Filter先得到:

$μ = M_{1}, σ^{2} = M_{2} - M_{1}^{2}$

$M_{1}$ 是粒子depth的平均值，
$M_{2}$ 是粒子depth平方的平均值。

Variance Shadow Mapping

考虑光源视角的深度为一个随机变量x。由切比雪夫不等式单边公式(推导²)，深度大于给定值t的概率有一个上界： $p (x \geq t) \leq \frac{σ^{2}}{σ^{2} + (t - μ)^{2}}$

论文¹假设把深度为d1的平面投影到深度为d2的平行平面，那么在深度为d1的平面边缘，可以假设投影深度正好为d2的概率为p，那么深度的期望为： $\begin{aligned} E (x) = p d_{2} + (1 - p) d_{1} \\ E (x^{2}) = p d_{2}^{2} + (1 - p) d_{1}^{2} \\ σ^{2} = E (x^{2}) - E (x)^{2} = (p - p^{2}) (d_{2} - d_{1})^{2} \end{aligned}$

深度小于d2的概率的上界： $P_{m a x} = \frac{σ^{2}}{σ^{2} + (d_{2} - μ)^{2}} = p$

化简后刚好为 p，当然这是一种理想情况，只有一次投影，一个遮挡物，但仍然可以用上述等式估算 p (其实就是一个微分级别的PCF值)。

但是，在Depth变化较大的区域(方差较大)，VSM会有缺陷(Light bleeding)。因为根据切比雪夫不等式，在方差较大的情况下，(t-μ)必须足够大，才能让不等式右边趋于0。于是又有了LVSM来解决这个问题。

Variance Depth Map

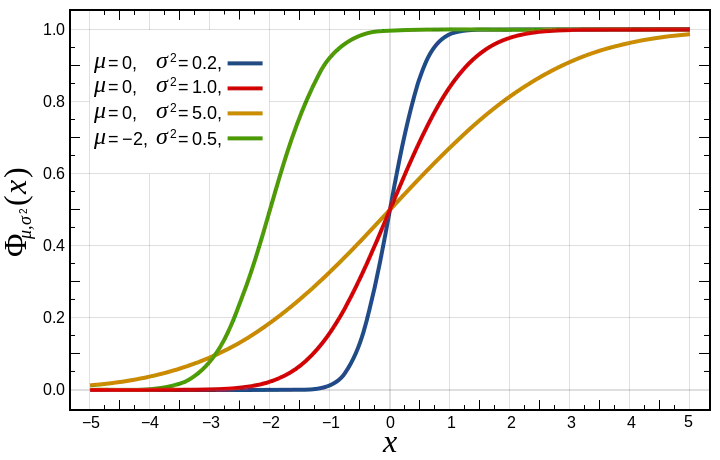
vdm_cdf

VDM³把概型改成了正态分布的CDF：[wiki]⁴ $C D F = \frac{1}{2} [1 + \erf (\frac{x - μ}{σ \sqrt{2}})]$

erf的计算参考龚大的文章⁵

VDM不光能用在粒子的渲染。凡是半透明、需要巨大填充率、颜色变化较平滑的内容，都可以用VDM来渲染，最后一次混合到全分辨率的场景上。比如大气效果、体积光，都符合这个条件。

其他

这类都是利用统计手段估计一个较合理的upsample混合方式，非常棒的想法。