期权入门

对波动率没兴趣的可从【关于期权】开始。
【3D绘图在手机safari渲染较慢，请等待】

完整代码：(py/iv.py)
本文数据：(https://github.com/noemotionLi/50ETF)

隐含波动率

通过Black-Scholes-Merton（BSM）期权定价模型，我们可以将期权的市场价格作为一个已知参数，进而反向计算出波动率。这种波动率，与基于股票历史价格计算出的历史波动率不同，被称为隐含波动率，即期权价格所隐含的波动率（IV）。

确定隐含波动率主要有两种方法：二叉树模型和BS模型。二叉树模型¹采用分阶段模拟的方法，对标的资产价格进行模拟，考虑多种可能的价格路径，并通过逆向工程计算出每条路径的隐含波动率。而BS模型则基于连续时间的假设，它假设标的资产价格遵循几何布朗运动等特定的统计过程，从而解析出隐含波动率。投资者可以根据自身的交易需求和市场状况，选择最合适的模型进行计算。

计算

为了便于计算，这里我们使用BS方程，更准确地说，考虑到分红因素，准确说我们使用的是BSM模型。首先，我们需要定义几个关键参数：

OP_C = 0.3557     # 当前期权价格
OP_S = 2.533    # 当前标的资产价格
OP_K = 2.25     # 行权价
OP_T = 16/365   # 期权剩余时间（年）
OP_r = 0.0264    # 无风险利率，用shibor近似
OP_q = 0.013675     # 年化分红率
OP_sigma = 0.23427  # 标的资产波动率
OP_option_type = 'C'# 期权类型

由 BS 定价公式，考虑分红的情况下：

$$ d_1=\frac{\ln{\left(S\left(t\right)/K\right)}+\left(r-q+\sigma^2/2\right)\left(T-t\right)}{\sigma\sqrt{T-t}} $$

$$ d_2=\frac{\ln{\left(S\left(t\right)/K\right)}+\left(r-q-\sigma^2/2\right)\left(T-t\right)}{\sigma\sqrt{T-t}}$$ $$=d_1-\sigma\sqrt{T-t} $$

看涨价格： $$ c=S\left(t\right)e^{-q\left(T-t\right)}N\left(d_1\right)-Ke^{-r\left(T-t\right)}N\left(d_2\right) $$

看跌价格： $$ p=Ke^{-r\left(T-t\right)}N\left(-d_2\right)-Se^{-q\left(T-t\right)}N\left(-d_1\right) $$

揉成一个函数：

def bsm_value(s,k,t,r,sigma,q,option_type):
    d1 = (np.log( s/k ) + ( r -q + 0.5*sigma**2 )*t ) / ( sigma*np.sqrt(t))
    d2 = d1 - sigma * np.sqrt(t)
    if option_type == 'C':
        value = s*np.exp(-q*t)*norm.cdf( d1) - k*np.exp(-r*t)*norm.cdf( d2)
    else:
        value = k*np.exp(-r*t)*norm.cdf(-d2) - s*np.exp(-q*t)*norm.cdf(-d1)
    return value

call_price = bsm_value(OP_S, OP_K, OP_T, OP_r, OP_sigma, OP_q, OP_option_type)
print(f"The call option price is {call_price}")
# The call option price is 0.28437779243840744

参数直接可得，分红率q可通过期权平价关系求出【公式1】：

$$ c\left(t\right)+Ke^{-r\left(T-t\right)}=p\left(t\right)+e^{-q\left(T-t\right)}S\left(t\right) $$

def iq(df): # 计算隐含分红率
    q = -np.log((df.c_c + df.k * np.exp(-df.r * df.t) - df.c_p)/(df.s)) / df.t
    return q

隐含波动率(IV)没有解析解，需要采用数值方法，这里图省事使用二分法：

def bsm_imp_vol(s,k,t,r,c,q,option_type):
    c_est = 0 # 期权价格估计值
    top = 1  #波动率上限
    floor = 0  #波动率下限
    sigma = (floor + top)/2 #波动率初始值
    count = 0 # 计数器
    while abs(c - c_est) > 0.000001:
        c_est = bsm_value(s,k,t,r,sigma,q,option_type)
        # 根据价格判断波动率是被低估还是高估，并对波动率做修正
        count += 1
        if count > 100: # 时间价值为0的期权是算不出隐含波动率
            sigma = 0
            break

        if c - c_est > 0: # f(x)>0
            floor = sigma
            sigma = (sigma + top)/2
        else:
            top = sigma
            sigma = (sigma + floor)/2
    return sigma

sigma = bsm_imp_vol(OP_S, OP_K, OP_T, OP_r, OP_C, OP_q, OP_option_type)
print(f"The call option imp_vol is {sigma}")
# The call option imp_vol is 0.8988456726074219

数据采用上证50ETF期权，由于是实盘数据，可能会有些异常交易：

def cons(d): # 条件约束，剔除噪点，尾盘拉砸
    if d['call_put'] == 'C':
        price = max(d.s - d.k * np.exp(-d.r * d.t), 0)
        return price < d.c and d.c < d.s
    else:
        price = max(d.k * np.exp(-d.r * d.t) - d.s, 0)
        return price < d.c and d.c < d.k * np.exp(-d.r * d.t)

df = df[df.apply(cons, axis=1)]

经过一揽子数据整合和清洗，计算得到：

k	30	65	156
2.2		0.2600861	0.237648
2.25	0.2858505	0.2477341	0.2313461
2.3	0.2750015	0.2398529	0.2248783
2.35	0.2566376	0.232811	0.2202015
2.4	0.2487907	0.2208595	0.2160244
2.45	0.2360687	0.2179432	0.2134342
2.5	0.2262917	0.2167473	0.2086182
2.55	0.2209816	0.2131195	0.2042828
2.6	0.2119827	0.2059288	0.202343
2.65	0.2068481	0.2079411	0.1987352
2.7	0.205265	0.2063732	0.1968079
2.75	0.2070389	0.2078018	0.1932144
2.8		0.2073631	0.1938143
2.85		0.2112999	0.193203
2.9		0.2122879	0.1935387
2.95		0.2180443	0.1947041
3.0		0.2252426
3.1		0.2379303
3.2		0.2603912
3.3		0.2766418
3.4		0.3038025
3.5		0.3298035
3.6		0.3529663

曲线

对于同一标的股票，用不同的到期日以及不同的行权价的多个期权的市场价格反向推算出的隐含波动率数值通常是不同的；以到期日和行权价作为两个维度，隐含波动率最为第三个维度，我们可以绘出一个隐含波动率曲面图。

将不同期限的期权合约及其在不同行权价格下的隐含波动率计算出来，每一个合约都能形成一个点，把所有的点连起来，就形成了波动率曲面。

先画一条线：

def smile_plot(df): # 波动率微笑
    df = df.set_index('k')
    df = df.stack().reset_index()
    df.columns = ['k', 'days', 'iv']
    fig = px.line(df, x="k", y="iv", color="days",line_shape="spline")
    fig.write_image("smile_plot.png")
    fig.write_json("smile_plot.json")

从曲线可以看出，波动率是随执行价格递增先是递减，至标的价格附近后，开始缓慢递增，这也是波动率微笑。黄金外汇的波动率是对称的微笑，股票的波动率微笑是不对称的，更准确的叫法是volatility skew（波动率倾斜），或者volatility smirk（波动率假笑）。至于形成原因，常见的解释是杠杆效应和恐慌情绪，但是也有人认为这就是一个市场的反应，没有特别的原因。

但 Black-Scholes（BS）模型的一个关键假设是标的资产的波动率是恒定的。为什么计算出的IV会有这种规律性结构变化呢？

这是因为在实际行情中，发生大涨大跌的概率要高一些，同时不温不火的概率也会高一些，种种因素导致隐含波动率呈现出“中间高两边翘”的特点，我们俗称叫“尖峰厚尾”²。

iv_n

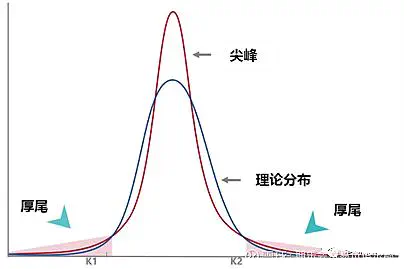
曲面

线动成面，这里用多项式方法进行了填充，使之圆润：

def im_surface(df): # 波动率曲面
    df = fitting(df) # 多项式拟合，详见代码文件
    df = df.set_index('k')

    y = np.array(df.index)
    x = np.array(df.columns)
    fig = go.Figure(data=[go.Surface(z=df.values, x=x, y=y)])

    fig.update_layout(scene = dict(
                    xaxis_title='剩余期限',
                    yaxis_title='执行价格',
                    zaxis_title='隐含波动率'),
                    autosize=True,
                    margin=dict(r=20, b=10, l=10, t=10),
                    )
    fig.write_image("im_surface.png")
    fig.write_json("im_surface.json")

更好看的绘制可以参考³，曲面一般会有以下几个特征：

同一到期日，行权价低，IV较高
短期波动率较高，远期波动率偏低

在交易上，很多投资者常常会进行一些波动率曲面交易，比如有种常见做法是通过在波动率曲面上寻找异常点，对冲成中性，以获取波动率回归正常的收益。但是在华尔街量化机器加持下，这种交易已经很难赚钱了。

曲面拟合(SVI)

波动率曲面的拟合是对经典Black-Scholes（BS）模型的重要补充和完善。其有助于确保市场中不存在无风险套利机会。平价套利、垂直套利和蝶式套利等策略为市场参与者提供了无风险套利的可能，而波动率曲面拟合模型能够有效识别市场中的定价偏差，并协助做市商进行调整，降低市场风险。

SVI模型，作为波动率曲面拟合中的佼佼者，最初由美林证券在1999年设计并投入使用，后由Gatheral在2004年的一次会议上向公众展示。该模型以其参数化的曲线形式，精确描述了波动率曲面的形态，并通过最小化与市场观测值之间的误差来拟合实际市场数据，捕捉市场波动率曲面的关键特征。SVI模型不仅能够避免日历套利和蝶式套利，而且在金融衍生品定价和风险管理中显示出其独特的价值⁴，具体实现可参考⁵ ⁶。

概率锥

在实际中，我们定义以下IV层级⁷：

执行价级 执行价对应的IV。
到期日级 将某一个到期日合约不同执行价下IV进行加权计算。
股票级 将各到期日下的IV再次加权计算，它用来计算股票预期波幅。

到此得到股票的IV(年化)，那如何预测股票的波动范围呢⁸？

$$S_{dst}=S*\sigma*\sqrt{T/12}$$

其实就是置信区间。

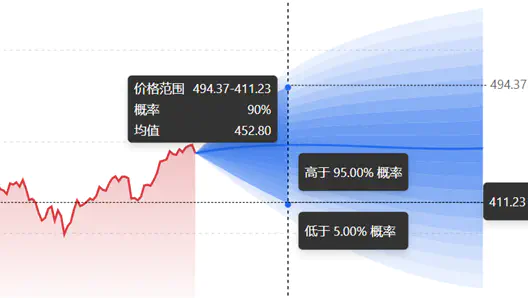
p_cone

VIX & SKEW

1993 芝加哥期权交易所（CBOE）推出了波动率指数VIX，反映S&P 500指数未来30天预期波动率，由于预期波动率多用于表征市场情绪，因此VIX也被称为“恐慌指数”。

其相关性的一些解释：

同向变动：稳健上扬->投机意愿增强->看涨期权价格上升->vix升
反向变动：巨幅下挫->迅速寻求避险->put价格bid up->vix spike

另一个角度，vix可以作为市场流动性指标。

下图为2015年到2020/6/14 VIX和SPX的对比，图中我们不难看出，每次SPX大跌的时候，VIX都会大涨。每当VIX达到相对高点时，SPX又开始触底反弹⁹：

vix

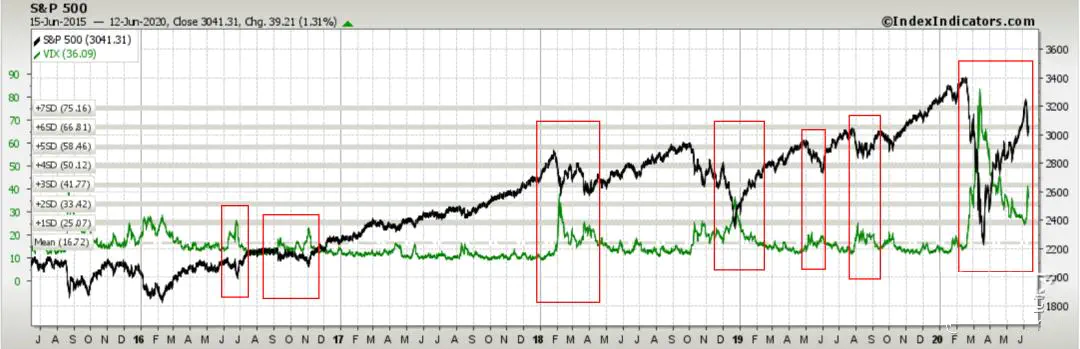
具体计算步骤¹⁰：

选取最接近平值的执行价两个，稍高于平价和稍低于平价各一个，即实值程度最小和虚值程度最小的执行价格;
然后取对应执行价格，近月和次近月的看涨期权(cal)和看跌期权(put)，共8个期权，计算每个交易对应8个期权的IV;
对波动率依次按看涨期权与看跌期权的平均、执行价价格价差加权平均和剩余到期期限三次加权平均;
最后即得到VIX指数;

2010年，芝加哥期权交易所（CBOE）推出的偏度指数（SKEW），该指数主要描述期权隐含波动率曲线斜率的走势情况，度量投资者对于市场收益不对称的预期，反映投资者对于市场尾部风险预期，对市场极端情况发生有预警功能，所以又称为“黑天鹅指数”，是波动率指数VIX的有效补充。

与VIX的计算方法十分相似，在挑选出标的期权后，计算出近月和次近月的偏度S(Skewness)，加权平均后使用插值法得到30日均值，最后进行简单代数变换得到偏度指数SKEW¹¹，具体实现可参考¹²。

关于期权

从数理逻辑的角度来看，几乎所有类型的交易/投资都可以归结为以下两类中的一类：trend following 或 mean reversion。

从几何的角度来看，股票的图形很像分形结构。而各种指标和信号无非是由股价走势和交易量变化构成的，所以trade指标本质上也是trade某些不断重复的几何形态。

从统计的角度来看，股价的走向整体是随机的(尤其是短线)，但是这里面又多少有一些非随机的因素。因为在一个真正的随机系统里面，总有一天你会回到原点，但事实上确实有不少人在市场持续的赚到钱了，所以它肯定不是一个真正的随机系统¹³。

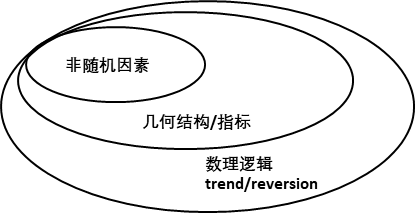
trade

如果是短线交易，要从市场持续的获取收益，你需要一个统计意义上能够产生稳定正收益的交易体系。举个简单的例子，比如trade均线，你发现某股票踩到50天均线之后有很大概率止跌回升，它的概率明显偏离了50%的随机概率；而这个非随机因素通过popcorn的几何形态表现出来；这个trade背后的数学逻辑则是mean reversion。这是非常鲜明的三个层次：

你是否发现了市场的非随机因素？
因素通过什么几何形态/指标表现出来？
背后的数学逻辑是什么？是否顺势？

而期权则是概率视角，其价格本身已经包含了非常丰富的信息：

期权市场已经帮你估算好了一笔交易的成功率【非随机因素】
期权市场背后的信息可以成为判断股价走势的指标【几何结构】
好的期权策略具有非常强的容错性

个人比较认可的几个期权认知阶段¹⁴
【付费内容，不展开 :) 】：

杠杆投机：按股票思维买入C/P，或者非常简单的组合。
组合策略：开始研究各种策略，以及它们的适用条件等等。
Greeks：意识到波动率和greeks的重要性，逐渐淡化策略和组合。
概率和风险：概率分布(波动率微笑)，风险回报比(theta/gamma)，以逸待劳。
账户整体表现和风险回报比：一盘大棋。

Edge

“Edge"代表了一种相对优势，即交易者在交易中相对于市场价格所掌握的额外信息或洞察力。它通常体现为期权的成交价格与其理论价格之间的差额。如果交易者能够以低于期权理论价格的成本买入期权，那么他们就拥有了"正Edge”，这通常被视为一种有利的交易位置。相反，如果成交价格高于理论价格，交易者则面临"负Edge"，这可能意味着他们支付了超出期权内在价值的价格¹⁵。

期权的理论价格可以通过多种复杂的金融模型来估算，例如二叉树模型，或者更现代的方法，如SVI模型，后者用于估计期权的隐含波动率。尽管这些模型可能对普通投资者来说过于复杂，但散户可以通过市场观察、交易软件的辅助或专业顾问的帮助来对期权的理论价值进行估计，并据此判断交易是否具有Edge。

卖方Edge来源：

期权市场整体来说是Overvalue的。
可以选择标的和随时解除合约。
判断期权合约是否高估/低估，判断不了的，不参与就成。

对于Edge的存在，可以这样验证，即同时卖出ATM Call和ATM Put（ShortStraddle），如果长期收益率为0，则证明定价完美。但通过历史回测，我们发现这种策略的长期收益甚至与SPY相当。

edge

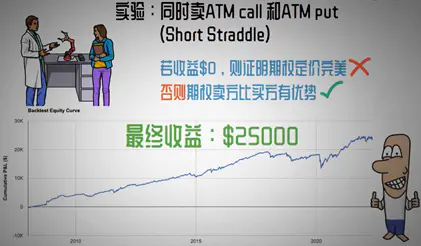
Delta Hedging

Delta中性策略是众多对冲策略的核心。在实施这一策略时，我们通常考虑的是相等头寸（Equivalent Stock Position, ESP）：

$$ ESP = 期权数量 × Delta × 每张对应正股数 $$

此外，比例看涨（Ratio Call）也是实现Delta对冲的一种常用工具。

再一个角度，由于期权的凸性：
(参见【Gamma & Theta】)

对于买家，相当于越跌越减仓
对于卖家，相当于越跌越加仓

Gamma Scalping

买方跨式(Long Straddle)是做多Gamma的策略，在此之上把Delta动态对冲到0附近，对冲的同时会实现不断的低买高卖，收割盈利，这就是传说中的Gamma Scalping¹⁶。

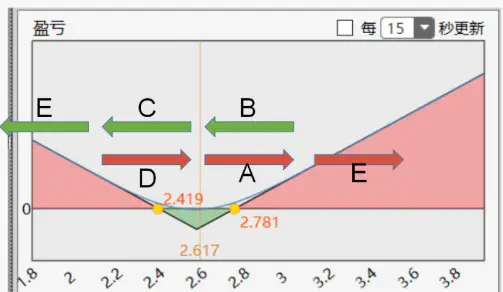
gamma

以50ETF为例，起手式，购入ATM的Call和Put，组成跨式策略。一开始Delta是在0左右，当开始A阶段快速上涨时，你是浮盈的，这时候Delta是正数，你需要做放空来对冲，把Delta降回0附近。当走B阶段回到原点时，此时Delta会是负数，把刚刚开的空头期货平仓出场，使Delta又回到0附近，借由这样操作，就完成了第一次获利入袋。同理C，D，都是捡钱逻辑。

然而，如果市场连续爆发走E路线，也无需担心。因为跨式策略的盈利潜力足以覆盖对冲操作的亏损，整体组合仍能盈利。

Scalping 也不是没有缺点，时间和波动率的消退对于它是个伤害，使用时注意判断。

Gamma & Theta

其实Gamma就是常说的凸性。
如果做多期权，可以获得期权的凸性，价值涨跌相较股票更好，但有theta的价值损耗；
如果做空期权，就等于放弃凸性，但可以获得theta带来的价值。

没有任何组合可以做到两者同时为正，因此对于任何期权交易而言，都可以看作为Gamma和Theta之间的取舍。

#	买方	卖方
Gamma	正，涨多跌少，上涨加速	负，跌多涨少，下跌加速
Theta	负，承担时间损耗	正，持续服务的补偿

值得注意的是Gamma Risk，即临近到期时候的ATM的Gamma最高，应尽量避免。

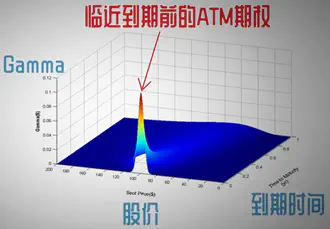
gamma risk

另一个是，Gamma squeeze，妖股们抽抽的力量之源。

再一个有趣的现象是，合成多头策略实际上是负Theta的。这种策略通过卖出Put和买入Call来模拟持有正股的效果。卖出Put的正Theta值通常小于买入Call的负Theta值，因此两者相加后，合成多头策略的Theta值仍然是负的。这种情况是必然的，因为如果合成多头策略的Theta值为正，那么持有正股的优势将不复存在。

最后，Gamma是Delta对股价S的偏导，那什么是对Theta的偏导呢，“Charm”，有兴趣可以查阅¹⁷。

Gamma & Vega

Long Gamma是指持仓Gamma值为正，表示做多股价实际波动，当股价真的从100元变到了110元或90元，那么做多实际波动的预期就实现了，在Gamma的维度上就赚钱了。而Long Vega是指持仓Vega值为正，表示的是做多股价的波动率，当你买入某个隐含波动率为25%的期权，两天后股价几乎一动不动，但隐含波动率却上升到了35%，这时做多隐含波动的预期就实现了，这部分赚的钱就是Vega带来的，而不是Gamma。

以上解释让人困扰，换个简单的比喻：位移和路程¹⁸。

vega

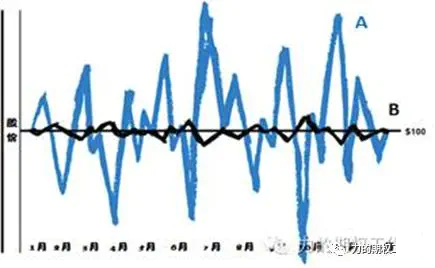
Max Pain & Stock Pinning

Stock Pinning
一些存在期权交易的股票，在期权到期日的星期五，股价都倾向于接触或者接近未平仓合同最多的行权价。

Max Pain
是对价格锁定的延展，那些活跃交易期权的股票，其价格往往倾向于向期权买家最不利的方向移动。换言之，股价似乎总是朝着使看涨期权（Call）和看跌期权（Put）价值最小化的行权价发展。这是因为在这种情况下，期权买家支付的权利金将遭受最大的损失，而期权卖家则能实现最大的利润。

应用条件¹⁹：

股票交易及期权交易量大的票
没有财报等惊喜事件
未平仓+交易量大 => 月期权好于周期权

这可能是由于玩家的Delta Hedging行为导致²⁰。具体预测和计算可以参见这个网站²¹。

如何利用？考虑theta层面的处理：

卖 Iron Condor²²
买 Butterfly

实践

期权异动

内幕交易在期权市场中可能更为隐蔽，因为期权具有杠杆效应，并且相较于股票市场，其监管可能不那么严格。期权的多种用途也为其提供了辩解的空间。同时，对于老鼠仓来讲也是极具价值的一类异动。以下以内幕交易为例阐述的异动分析方法：

期权的交易量，出现不同寻常的增加
- Relative Volume(RV) > 3
  需要排除：公司财报或者关键数据
- Open Interest
  如果RV上升，但Open Interest并没有，大概率是机构在调仓
异动涉及的期权Delta在0.2到0.4之间
- 过低：WSB关注的期权
- 过高：一般是机构用来代替正股
- 区间内：Gamma作用非常大，有利于买方以小博大
个股的IV，处于上升的状态中
- 内幕交易->大量买单->推升IV
- IV没升高，大概率是卖期权/平仓
- 观察IV skew，判断IV的影响和方向
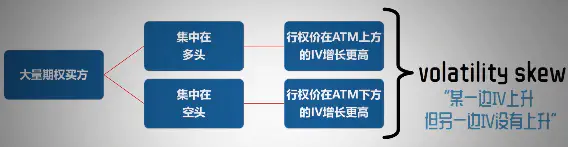
总之，option flow必须按照观察到的方向流动²³
- 没方向：说明有人赌波动性

最佳风险比

经过回测，SellPut长期最优(本文不展开)：
SellPut > BullPutSpread > LongCall

> 行权价
OTM：熊市好
ATM：穿越牛熊
ITM：牛市好

> Roll Over
钉住Delta(Delta不变，每次ATM)：
穿越牛熊，安心投资

HTS(Hold the strike)：
熊市，绝对不能用，牛市，收益极高

> 杠杆率
1.5-2倍杠杆收益风险比最佳

计算方法：
(P-)仓位=行权价 x 100
杠杆率 = 行权价 x 100 / 本金

> 动态仓位
VIX越高越减仓(越跌越减仓)
基础VIX = 25时收益风险比最佳

ccput3

> SellPut or CC ？

通过前文提及的平价关系【公式1】，在ATM情形下化简得：
【股票】(S+)=【买入】(C+) +【卖出】(P-)

这就是所谓的合成多头策略，移项可得：
【Sell Put】(P-) = (S+) + (C-)【CC】

卖出看跌等同于持有备兑看涨，不考虑税务问题，如何选择？
【大盘系统性Sell Put，个股灵活CC】

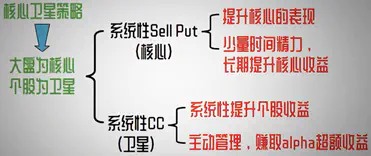
ccput1

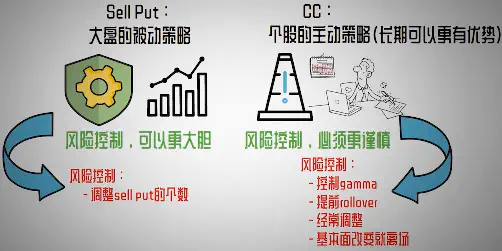
ccput2

> 小结：平衡型
有动态调仓，越跌越减
1.5-2倍杠杆
rollover至ATM
大盘Sell Put，个股灵活CC

实际使用可以在平衡策略上按需调整。此外CC也可以在LEAPS²⁴的加持下变为PMCC，此处不展开。

到此，你可能会觉得这非常不可思议，头脑在飞速运转到底哪里不合理。万一股价暴涨了怎么办呢？是不是只有股价下跌了才真正能赚到钱呢？会这么想，说明你还没有摆脱股价的思维限制。事实上有大量回测表明，ATM covered call是收益风险比最高的看涨策略之一²⁵。

其他策略

最佳抄底

抄底面临的两大问题：

反转何时到来
还要下跌多久

Risk Reversal(RR)：
Long OTM Call + 卖Short OTM Put

Long Call(看涨) + Sell Put(看涨) = 看涨
Sell Put消减了Theta，
同时提供了Finance
下跌：Put贵，Call贱，
上涨：Call贵，Put贱

短期对冲

择时还是对冲？：躺！

海鸥策略：利用期权到期时的效果，尽可能弥补潜在的亏损。

100正股 + Long Put + 上卖Call + 下卖Put
Long Put对冲，卖出C/P进行Finance

定量思维

风险度量：

Total Return：总收益
Annual Return：年化收益
Variance：方差
Volatility：标准差
Sharpe Ratio：夏普率
Max loss in one day：单日最大回撤
Max Drawdown：最大回撤
Roman：Return/Max Drawdown，总收益/最大回撤

Beta(超额)与R2(相关性)²⁶
在实际应用中，投资者可能会同时考虑这两个指标来评估股票或投资组合的表现。例如，一个高Beta值的股票可能需要更高的预期回报来补偿其较高的风险，而一个高R2值表明该股票的表现与市场紧密相关，有助于投资者更好地理解其在市场波动中的表现。

投资组合的风险²⁷
标普500指数(SPX)被认为最能代表市场。投资组合的风险可以通过该指数来衡量，比如用SPX指数计算组合的Beta值。由于Beta值是波动性的参考，因此可以使用SPX期权对冲整个组合，而不是单独的股票头寸。你当然需要考察单个股票(如IBM或沃尔玛公司)的Beta值，但通常考虑整体更有意义。

未来尝试

大盘SellPut，新手期个股暂不考虑期权
ShortStraddle增加趣味性
风险比视角，越跌越减仓

数据源备忘

新浪获取：
https://github.com/yewenwu123/pythonOption/tree/main

yahoo(需要科学上网)：

# https://blog.csdn.net/weixin_44195690/article/details/128983977
import yfinance as yf
data = yf.download("SPY AAPL", period="1mo",proxy="http://127.0.0.1:1080")

Learn it all
Hunt for what you like
Widen your edges