最近看UE分享的[Temporal AA]1 时卡在SpecularAA上,引出下面这些。
Specular Aliasing
原因是采样率, 非实时渲染中,因为采样率很高,对于一个pixel,积分发生在计算完成之后, 实时渲染的采样率极其有限,一般只有1,积分发生在建立mipmap的时:
$$spec = \sum {\left (\frac {N_{i} \cdot H}{|N_{i}|} \right )^s} \xrightarrow{Mipmap} \left (\frac {(\sum {N_{i}}) \cdot H}{|\sum {N_{i}}|} \right )^s$$
很显然这两个不等价,造成了Specular Aliasing。

有知乎大神从TA的角度解释了一通2,但我更关注由此引出的mipmap问题。
LEAN Mapping
LEAN Mapping(包括进一步发展的CLEAN Mapping)3的出现就是为了解决这个问题。
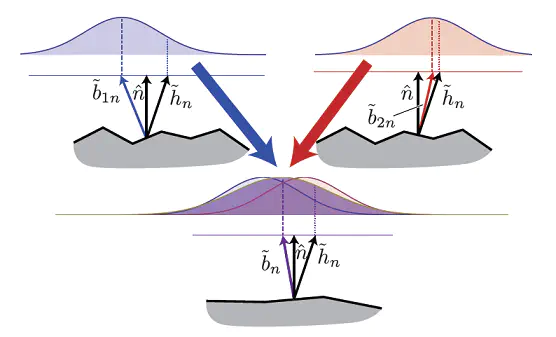
给出一张图,公式就不贴了,全是矩阵运算, 大意是,构建时协方差之类都保存下来,用以运行时候复原分布。
Good 还原度好,各向异性。
Bad LEAN需要5个通道(CLEAN需要4个通道),其中有些通道要求16-bit, Tangent Space, Blinn-Phong需要改成Beckmann。
本文重点不是这,不展开了,具体可以看这篇综述[Rock-Solid Shading]4
Mipmapping Normal Maps
来自Toksvig 2005,Mipmapping normal maps5
如果一个区域内的normal什么方向都有,那么平均normal就会很短,方差就较大,所以需要降低高光。
首先,在生成mipmap时候生成一个平均normal长度Na, 作者统计后决定,按下面关系将方差 $\sigma$ 信息编码进NaLength中:
$$ |N_{a}| = \frac{1}{1+\sigma^{2}} \Leftrightarrow \sigma^{2} = \frac{1-|N_{a}|}{|N_{a}|} $$
再引入一个近似,令$\sigma_{s} = s^{-\frac{1}{2}}$:
$$\cos ^{s} {\alpha} \approx e^{-\frac{a^2}{2} s} = e^{-\frac{a^2}{2 \sigma_{s}^2}}$$
可以看到,的确近似(cos:红色,s=1:绿色外圈,s=40:绿色叶状):
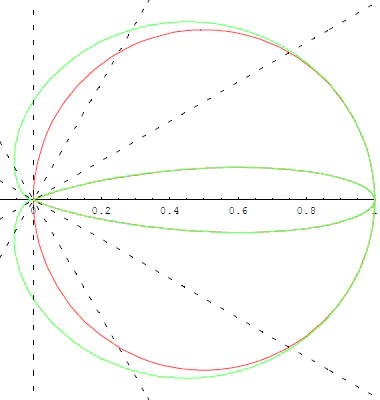
于是成功将次方项转为高斯函数。 再加个高斯核给它施加影响(相当于做一次模糊),由于高斯函数卷积特性也就是对方差项做个加法,论文中是用自己的方差带入计算,得到新高光项 s':
$$ \sigma_{{s}'} ^2 = \sigma ^2 + \sigma_{s} ^2 \Rightarrow {s}'= \frac{1}{1+s \sigma^2} s $$
作者用自己的大名定义了一个系数,“Toksvig factor”:
$$f_{t} = \frac{1}{1+s\sigma^2} = \frac{|N_{a}|}{|N_{a}| + s (1-|N_{a}|)}$$
修改之后的specular变成了:
$$spec = \frac{1+f_{t} s}{1 + s}\left (\frac{N_{a}\cdot H}{| N_{a}|} \right )^{f_{t} s}$$
由于,半球积分不为1:
$$\int_{hemi} \cos^{s} \alpha d \alpha = \frac{ 2\pi}{s+1}$$
需要保能量:
$$spec = \frac{1+f_{t} s}{2\pi}\left (\frac{N_{a}\cdot H}{| N_{a}|} \right )^{f_{t} s}$$
然而直接除并不对,Wild West开发人员提供了一种解法6:
$$spec = \frac{f_{t} s+2}{8}\left (\frac{N_{a}\cdot H}{| N_{a}|} \right )^{f_{t} s}$$
同时他们也给出了实现方法。
高大上的模糊过程 :)
其他
Leanmap 较为重度,但还原性较好。 Mipmapping Normal Maps 简单粗糙够用。 Wild West6最后给出了两者结合的方向,以后再研究了。
此外,龚大的做法是在建立normal map的mipmap时,不但对生成的平均normal做normalize,而且把它的长度存到另一张texture,称为NaLength map。在渲染的时候,读取NaLength的内容,计算出ft,这样对原有流程改动很小7。